凸包とは?
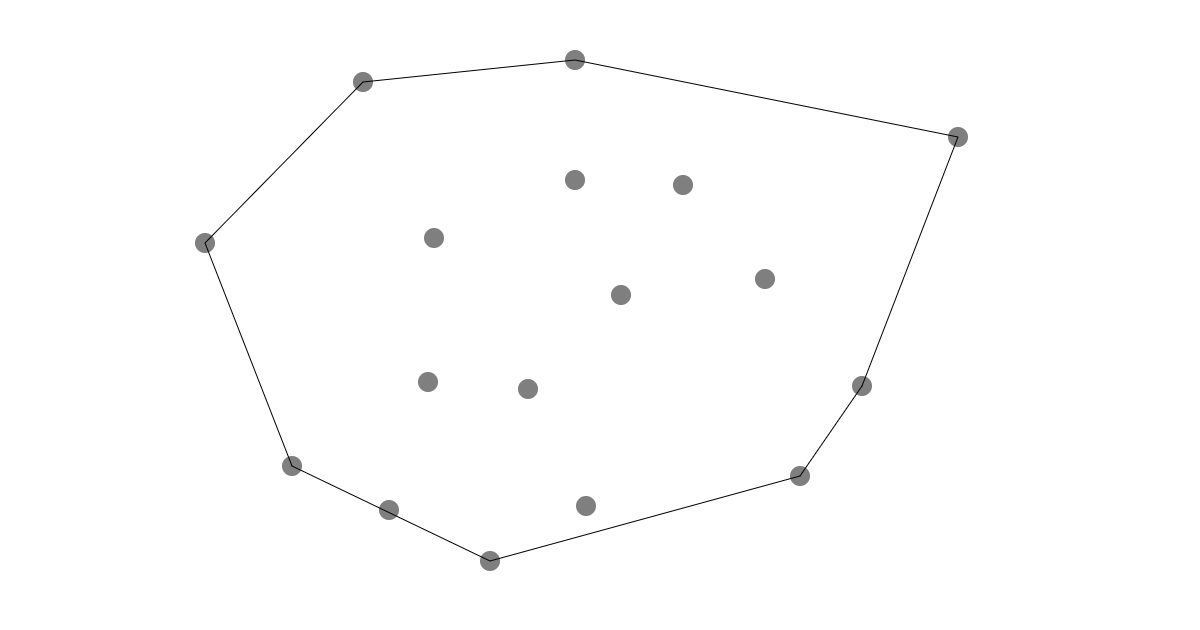
まずはじめに凸包について、凸包というのは「与えられた点をすべて包含する最小の凸多角形のこと」です。イメージとしては以下の画像ですね。

こんなの何に使うの?って思うかもしれませんが、多角形と点の当たり判定(例えば、多角形ボタン UI とのタッチ判定)に使用出来たり、グラフィックスを扱うプログラムでは意外と応用範囲が広いです。今回は、この凸包を計算するプログラムを書いてみます。
凸包のアルゴリズム:ギフト包装法
凸包を求めるアルゴリズムの中で、最も直感的でわかりやすいのが、ギフト包装法(Gift wrapping algorithm)です。このアルゴリズムの考え方としては、
- 最も y 座標が小さく、その中で x も最も小さいものを求めて注目点とする
- 次の点を求めるために、注目点ほか全ての点との偏角を求めて、最も左にあるものを選ぶ
- 一周するまで繰り返す
というものです。具体的なソースコードをみていきましょう。
最も y 座標が小さく、その中で x も最も小さいものを求める
ここでは points という配列に、点情報(x, y) が入っているものとします。まずは、配列の先頭の点情報を注目点と仮に定め、あとはその点と他のすべての点を比較して、注目点を更新していきます。
let basep = points[0];
points.forEach(point => {
if (basep.y > point.y || ((basep.y == point.y) && basep.x > point.x)) {
basep = point;
}
});上記のようなコードでループが完了すれば、注目点が basep に格納されます。
次の点を求めるために、注目点ほか全ての点との偏角を求めて、最も左にあるものを選ぶ
最も左にある点を求めるには、外積の計算を行います。
チェック対象の点(A)と、現時点で最も左にある点(B)、比較対象の点(C)とした場合、ベクトル AB と ベクトル AC の外積を計算します。この計算結果が正なら直線 AB に対して点 C は左側にあると判定できます。
let next = function(points, checkp) {
let nextp = points[0];
for (let i = 1, max = points.length; i < max; ++i) {
let point = points[i];
if (checkp == nextp) {
nextp = point;
} else {
let v = (checkp.x - nextp.x) * (checkp.y - point.y) - (checkp.x - point.x) * (checkp.y - nextp.y);
let ab = (checkp.x - nextp.x) * (checkp.x - nextp.x) + (checkp.y - nextp.y) * (checkp.y - nextp.y);
let ac = (checkp.x - point.x) * (checkp.x - point.x) + (checkp.y - point.y) * (checkp.y - point.y);
if (v > 0 || (v == 0 && Math.abs(ac) > Math.abs(ab))) {
nextp = point;
}
}
}
return nextp;
};こちらのコードでは、すべての点情報が格納された配列 points と チェック対象の点 checkp を渡すと、points に含まれる点情報から、checkp の最も左側にある点情報を返す next 関数として定義しました。
一周するまで繰り返す
最後はすべての点に対して計算を繰り返し、点が基準点に戻ってきたら処理は完了です。
let result = [];
let lastp = basep;
do {
result.push(lastp);
lastp = next(points, lastp);
} while(basep != lastp);
result.push(basep);こちらのコードでは、result 配列に凸包を構成する点情報が格納されていきます。
実行サンプル
クリックすると点が作成され、それらの点をすべて包含する最小の凸多角形を描画します。
ソースコード
今回書いたソースコードの全文は以下にあります。Unlicense として公開していますので、どなたでも自由にお使いいただけます。


コメント