この記事では、扇形と点の当たり判定の詳細な実装方法について説明します。扇形と点の判定ができれば、ゲーム上のキャラクターの視野範囲を表現することができます。
判定方法
扇形と点の当たり判定を行うためには、以下の2つの条件を両方とも満たす必要があります。
- 扇形の方向ベクトルと点から扇の中心へのベクトルを結んだベクトルのなす角が、扇の範囲(角度)より小さい。
- 扇形と点の中心からの距離が、扇の半径よりも小さい。
実装
以下に、上記の判定方法に基づいて、扇形と点の当たり判定を行う実装の詳細を示します。
1. 準備
実装には、扇形と点それぞれの情報を格納する構造体やクラスを準備します。これらの情報を基に判定を行います。今回は外部ライブラリを使用していませんので、一般的なクラスであっても自前で定義しています。何か数学系ライブラリを使用するのでしたら、適宜、置き換えても問題ありません。
Vectorクラス
Vectorクラスは、2次元ベクトルを表すためのクラスです。ベクトルの演算や描画を行うためのメソッドが定義されています。lengthメソッドはベクトルの長さを計算し、normalizeメソッドはベクトルを正規化(長さを1にする)します。また、ベクトルのスケーリングや距離の計算も行えます。
class Vector {
constructor(x = 0, y = 0) {
this.x = x;
this.y = y;
}
draw(context, v0, width, color = '#00ff00') {
context.beginPath();
context.moveTo(v0.x, v0.y);
context.lineTo(v0.x + this.x, v0.y + this.y);
context.strokeStyle = color;
context.lineWidth = width;
context.stroke();
}
length() {
return Math.sqrt(this.x * this.x + this.y * this.y);
}
normalize() {
let len = this.length();
return new Vector(this.x / len, this.y / len);
}
scale(factor) {
return new Vector(this.x * factor, this.y * factor);
}
distance(vector) {
return new Vector(this.x - vector.x, this.y - vector.y);
}
}Arcクラス
Arcクラスは、円弧(扇形)を表すためのクラスです。円弧の中心座標、半径、開始角度、終了角度を保持します。drawメソッドによって、指定した属性で円弧を描画します。
class Arc {
constructor(x, y, radius, startAngle, endAngle) {
this.x = x;
this.y = y;
this.radius = radius;
this.startAngle = startAngle;
this.endAngle = endAngle;
}
draw(context, color='#f3f3f3') {
context.beginPath();
context.moveTo(this.x, this.y);
context.fillStyle = color;
context.arc(this.x, this.y, this.radius, this.startAngle, this.endAngle, false);
context.fill();
}
}ヘルパー関数
ソースコード内には、いくつかのヘルパー関数が定義されています。これらの関数は、数学的な計算やランダム値の生成を行うために使用されます。
deg2rad:度数をラジアンに変換する関数。rad2deg:ラジアンを度数に変換する関数。orgfloor:数値を指定の小数点以下の桁数に切り捨てる関数。randomMinMax:指定の範囲内でランダムな数値を生成する関数。
2. 二つのベクトルの準備
点と扇形の中心とのベクトルを計算し、その長さを求めます。
// 扇形の中心座標(今回はキャンバスの中心)
const arcCenterPos = new Vector(canvasWidth / 2, canvasHeight / 2);
// 当たり判定をする点の座標(今回はマウス座標が入ります)
mousePos = { x:..., y: ...};
// 点と扇形の長さを取得
let arcToPoint = arcCenterPos.distance(mousePos);3. 扇の方向ベクトルの準備
扇形の方向ベクトルを計算します。これは、扇形の中心から扇形の方向へのベクトルで、ちょうど扇を二等分する線となります。以下の図では緑の線がそれにあたります。
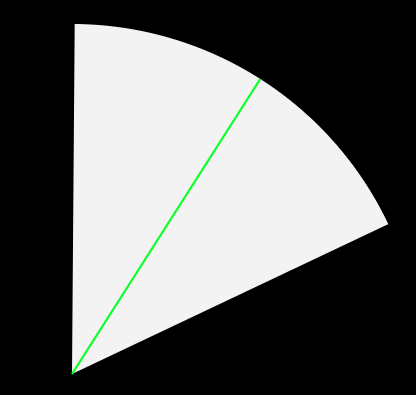
// 扇形 (開始角度 + 終了角度) / 2 で中央の角度を求める
const arcMidRadian = (arc.startAngle + arc.endAngle) / 2;
// 角度からベクトルを求める
let arcDirectionVector = new Vector(Math.cos(arcMidRadian), Math.sin(arcMidRadian));
// ベクトルを正規化
arcDirectionVector = arcDirectionVector.normalize();4. 内積の計算
点と扇形のベクトルと扇形の方向ベクトルの内積を計算します。
let dot =
arcToPointNormalized.x * arcDirectionVector.x +
arcToPointNormalized.y * arcDirectionVector.y;5. 扇の範囲の cos 値の計算
扇形の範囲から cos 値を計算します。範囲の角度を2で割って cos を求めます。
let cos = Math.cos((arc.endAngle + Math.PI - arc.startAngle + Math.PI) / 2);6. 判定する
これで必要な情報が揃いました。内積の cos 値と扇形の範囲の cos 値を比較し、点が扇形の範囲内にあるかどうかを判定と、扇形と点の中心からの距離が扇の半径よりも小さいかを判定します。
// 点が扇形の範囲内にあるか && 扇形と点の中心からの距離が扇の半径よりも小さい
let isHit = dot < cos && arcToPoint.length() <= arc.radius;条件が成立すれば、点が扇形の範囲内に存在すると判定できます。逆に、いずれかの条件が満たされない場合は、点が扇形と当たっていないことになります。
ソースコード
今回書いたソースコードの全文は以下にあります。



コメント